[转]Unity Shader Bible翻译学习

第一章 | 着色器编程语言介绍

入门知识

1.0.1 | 多边形物体的属性

许多年前，当我刚开始学习 Unity 中的着色器时，有几个原因导致我难以理解书本上的内容。我仍然记得有一天，我希望理解语义 POSITION[n] 的操作，但关于它的介绍只有短短一句：

物体空间中的顶点位置。

什么是物体空间中的顶点位置？这时我意识到，在开始学习之旅前我必须先了解一些基础知识。

根据我的经验，至少有四个基本方面有助于理解着色器及其结构，如多边形物体的属性、渲染管线的结构、矩阵以及坐标系。

1.0.1 | 多边形物体的属性

多边形（polygon） 一词来自希腊语，由“多”（poly）和“角”（gnow）组成。根据定义，多边形是指平面的封闭几何图形，由大于2条线段组成，且首尾相连划出的形状。

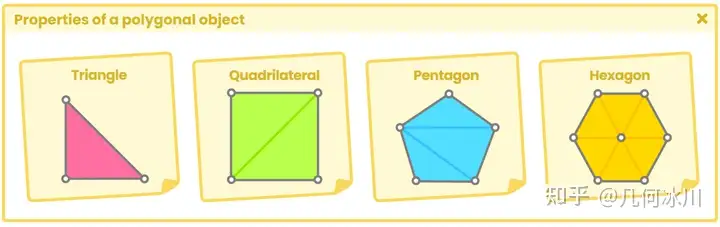
Fig. 1.0.1a

基本体（primitive） 是由多边形构成的三维几何对象，在诸如Unity、Maya、Blender等不同的开发软件中用作预定义对象。最常见的基本体有球体、正方体、四边形、圆柱体和胶囊体等。这些物体虽然形状各异，但属性相似：它们都有顶点、切线、法线、UV 坐标和颜色，这些属性被存储在一种名为 “ 网格（mesh） “的数据类型中。

我们可以在着色器中独立访问所有这些属性，并将它们保存在向量中（例如 float4 pos: POSITION [n]）。这样做的好处是我们可以修改它们的值，从而编写出令人兴奋的效果。为了更好地理解这一概念，我们将给出关于多边形物体属性的定义。

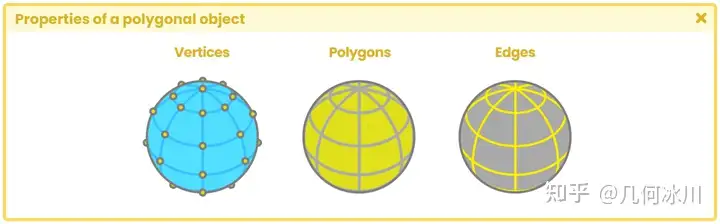
Fig. 1.0.1b

1.0.2 | 顶点

1.0.3 | 法线

1.0.4 | 切线

1.0.5 | UV坐标

1.0.6 | 顶点颜色

1.0.7 | 渲染管线架构

1.0.8 | 应用阶段

1.0.9 | 几何处理阶段

1.1.0 | 光栅化阶段

1.1.1 | 像素处理阶段

1.1.2 | 渲染管线类型

1.1.3 | 前向渲染

1.1.4 | 延迟渲染

1.1.5 | 我该用哪种渲染管线？

1.1.6 | 矩阵与坐标系统

Unity中的Shader

2.0.1 | 什么是着色器(shader)？

2.0.2 | 编程语言介绍

2.0.3 | 着色器的种类

2.0.4 | 标准表面着色器

2.0.5 | 无光照着色器

2.0.6 | 屏幕特效着色器

2.0.7 | 计算着色器

2.0.8 | 光线追踪着色器

属性、命令与函数

3.0.1 | 顶点/片元着色器的结构

3.0.2 | ShaderLab着色器

3.0.3 | ShaderLab的属性

3.0.4 | 数字与滑条类型

3.0.5 | 颜色与向量类型

3.0.6 | 纹理类型

3.0.7 | 自定义材质属性绘制器

3.0.8 | MPD开关

3.0.9 | MPD关键词枚举

3.1.0 | MPD枚举

3.1.1 | MPD指数滑条与整数范围

3.1.2 | MPD空白与标题

3.1.3 | ShaderLab子着色器

3.1.4 | ShaderLab标签

3.1.5 | 队列标签

3.1.6 | 渲染类型标签

3.1.7 | SubShader混合

混合（Blending）是将两个像素处理成一个的过程，是内置渲染管线（Built-in）与可编程渲染管线（SRP）都兼容的一种命令。

*混合 *发生在“ 合并（merging） ”的阶段，它将像素的最终颜色（在片元着色器阶段处理后的像素）与像素的深度结合在一起。这个阶段位于渲染管线的末端，在片元着色器阶段之后，是执行模版缓冲（stencil-buffer）、深度缓冲（z-buffer）和颜色混合（color blending）的地方。

混合属性不会被写在新建的默认着色器里，因为这是一个通常被使用在透明物体中的可选功能，比如说当我们必须在一个像素前绘制另一个不透明度较低的像素时。

混合的默认值是“Blend Off”（不开启混合），但我们可以通过设置它来实现不同类型的颜色混合效果，就像在 Photoshop 中的混合效果那样。

混合的语法如下所示：

1
Blend [SourceFactor] [DestinationFactor]

“ 混合 ”是一个函数，需要两个输入，经过一个计算公式得到屏幕上的最终颜色。根据 Unity 的官方文档，定义 混合结果的值的等式如下：

B = SrcFactor * SrcValue [OP] DstFactor * DstValue.

为了理解这个公式，我们需要记住这个顺序： 首先是 片元着色器阶段 ，然后是可选的 合并阶段 。

“SrcValue” (源颜色）代表的是经过片元着色器处理的像素的RGB值。

“DstValue” (目标颜色) 代表的是已经写入“目标缓冲”的像素的RGB值，目标缓冲更常见的名字是渲染目标（SV_Target）。当我们没有在着色器中设置混合选项时，源颜色会直接覆盖目标值。如果我们设置了混合，源颜色与目标颜色就会混合产生一个新的颜色，再覆盖先前的目标颜色。

“SrcFactor” (源系数) and “ DstFactor “ (目标系数) 都是一个三维向量，它们主要的功能是修改源颜色和目标颜色来实现有趣的效果。

我们能在Unity官方文档（ShaderLab 命令：Blend - Unity 手册）找到一些系数：

• Off , 禁用混合选项。
• One , (1, 1, 1)。
• Zero , (0, 0, 0)。
• SrcColor 等于源颜色的RGB值。
• SrcAlpha 等于源颜色的透明度。
• OneMinusSrcColor , 1 - 源颜色的RGB值 (1 - R, 1 - G, 1 - B)。
• OneMinusSrcAlpha , 1 - 源颜色的透明度 (1 - A, 1 - A, 1- A)。
• DstColor 等于目标颜色的RGB值。
• DstAlpha 等于目标颜色的透明度。
• OneMinusDstColor , 1 - 目标颜色的RGB值 (1 - R, 1 - G, 1 - B)。
• OneMinusDstAlpha , 1 - 目标颜色的透明度 (1 - A, 1 - A, 1- A)。

值得一提的是，透明度（Alpha）通道的混合与 RGB 颜色混合的方式相同，但由于不常用，所以是在一个独立的流程中完成的。如果不执行透明度混合，写入渲染目标上的过程也会得到优化。

让我们来理解理解上面的这段话。

假设我们现在有一个RGB值为 [0.5R, 0.45G, 0.35B] 的像素，已经经过片元着色器的处理，所以这个像素现在就是我们的源颜色。现在，我们把这个源颜色乘上系数“*SrcFactor * One ”（即 [1, 1, 1]），由于每个数字乘以 “1” 的结果都是它本身，因此，源系数和源颜色之间的结果就等于 [0.5R, 0.45G, 0.35B] 。

B = [0.5R, 0.45G, 0.35B] [OP] DstFactor * DstValue.

“OP”指的是我们要执行的操作，一般默认设为加法（Add），如下所示：

B = [0.5R, 0.45G, 0.35B] + DstFactor * DstValue.

到这一步之后，再来看看已经写入颜色缓冲中的目标颜色（假设为 [0.5R、0.45G、0.35B]）。让我们将目标系数设置成“DstFactor DstColor ”，该系数等于当前目标颜色的 RGB 值，则有：

DstFactor [0.5R, 0.45G, 0.35B] * DstValue [0.5R, 0.45G, 0.35B] = [0.25R, 0.20G, 0.12B].

所以最后输出的像素颜色是：

B = [0.5R, 0.45G, 0.35B] + [0.25R, 0.20G, 0.12B]. B = [0.75R, 0.65G, 0.47B]

如果我们想要在着色器中开启混合，我们就需要使用到混合指令、源系数和 目标系数 ，语法如下所示：

1
2
3
4
5
6
7
8
9
Shader "InspectorPath/shaderName" 
{ 
    Properties { … } 
    SubShader 
    { 
        Tags { "Queue"="Transparent" "RenderType"="Transparent" } 
        Blend SrcAlpha OneMinusSrcAlpha 
    } 
}

如果我们想在着色器里使用混合就必须添加和配置“ 渲染队列（Render Queue） ”。我们已经学习过默认的“ 队列（Queue） ”标签是“ 几何（Geometry） ”，代表我们的物体是不透明的。如果我们想要让物体看起来有透明的感觉，就需要把“队列”标签设置为“ 透明（Transparent） ”，再设置混合选项。

最常见的几种混合命令如下所示：

• Blend SrcAlpha OneMinusSrcAlpha 传统透明度混合
• Blend One One 加法
• Blend OneMinusDstColor One 软加法
• Blend DstColor Zero 乘法
• Blend DstColor SrcColor 2x 乘法
• Blend SrcColor One 叠加
• Blend OneMinusSrcColor One 柔光
• Blend Zero OneMinusSrcColor 反色

另一种配置混合的方式是通过“UnityEngine.Rendering. BlendMode”，它允许我们从检查器中更改材质的混合效果。但首先，我们必须在属性中添加 “ Toggle Enum “，然后声明源系数和目标系数。

语法如下所示：

1
2
3
4
[Enum(UnityEngine.Rendering.BlendMode)] 
    _SrcBlend ("Source Factor", Float) = 1 
[Enum(UnityEngine.Rendering.BlendMode)] 
    _DstBlend ("Destination Factor", Float) = 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Shader "InspectorPath/shaderName" 
{ 
    Properties 
    { 
        [Enum(UnityEngine.Rendering.BlendMode)] 
        _SrcBlend ("SrcFactor", Float) = 1 
        [Enum(UnityEngine.Rendering.BlendMode)] 
        _DstBlend ("DstFactor", Float) = 1 
    }
    SubShader 
    { 
        Tags { "Queue"="Transparent" "RenderType"="Transparent" } 
        Blend [_SrcBlend] [_DstBlend] 
    } 
}

混合选项可以写在子着色器或** Pass** 语义块中，具体写在哪里取决于 pass 的数量和我们最终想要取得的结果。

3.1.8 | SubShader透明度遮罩

3.1.9 | SubShader颜色遮罩

3.2.0 | SubShader剔除与深度测试

3.2.1 | ShaderLab剔除

3.2.2 | ShaderLab深度写入

深度写入这个命令控制了物体表面像素写入 Z 缓冲（深度缓冲）的这一过程。它允许我们忽略或写入物体与相机间的深度。深度写入有两个可以设置的值，分别是开启（On）和关闭（Off），默认值为开启。我们通常在处理透明度时（例如混合）会关闭深度写入。

• ZWrite Off 处理透明度时
• ZWrite On 默认值

为什么我们需要在处理透明度时禁用 Z 缓冲？主要是因为半透明像素叠加（深度冲突）的问题。当我们处理半透明物体时，GPU 通常不知道哪个物体位于另一个物体前面，因此当我们在场景中移动摄像机时，像素之间会产生奇怪的重叠效果。要解决这个问题，我们只需将深度写入命令设置为“ 关闭（Off） ”，停用 Z 缓冲区即可：

1
2
3
4
5
6
7
8
9
10
Shader "InspectorPath/shaderName" 
{
    Properties { … } 
    SubShader 
    { 
        Tags { "Queue"="Transparent" "RenderType"="Transparent" } 
        Blend SrcAlpha OneMinusSrcAlpha 
        ZWrite Off 
    } 
}

深度冲突（Z-fighting）发生在两个或多个物体具有相同的深度时，导致 Z 缓冲中的值完全相同。

https://picx.zhimg.com/80/v2-f16fe9a84f37cb76f4808e66cb3c24e8.png

Fig. 3.2.2a

接着，当尝试在渲染管线末端渲染这些像素时，就会出现上图所示的这种效果。由于 Z 缓冲无法确定究竟哪个物体位于另一个物体的后面，就会产生这些闪烁的线条。线条的形状会根据摄像机的位置而改变。

想修复这个问题，我们只需要用命令关闭深度写入（ZWrite off）、禁用 Z 缓冲区即可。

3.2.3 | ShaderLab深度测试

深度测试（ZTest）通常用于在有多 pass 的着色器中生成颜色和深度差异。该属性有七个不同的值，分别是：

• Less.
• Greater.
• LEqual.
• GEqual.
• Equal.
• NotEqual.
• Always.

它们与比较操作相对应。

ZTest Less : (<) 绘制位于现有几何体前面的几何体。不绘制位于现有几何体相同距离或后面的几何体。

ZTest Greater : (>) 绘制位于现有几何体后面的几何体。不绘制位于现有几何体相同距离或前面的几何体。

ZTest LEqual: (≤) 默认值。绘制位于现有几何体前面或相同距离的几何体。不绘制位于现有几何体后面的几何体。

ZTest GEqual : (≥) 绘制位于现有几何体后面或相同距离的几何体。不绘制位于现有几何体前面的几何体。

ZTest Equal : (==) 绘制位于现有几何体相同距离的几何体。不绘制位于现有几何体前面的或后面的几何体。

ZTest NotEqual : (! =) 绘制不位于现有几何体相同距离的几何体。不绘制位于现有几何体相同距离的几何体。

ZTest Always : 不进行深度测试。绘制所有几何体，无论距离如何。

为了理解深度测试，我们将做以下练习： 假设场景中有两个物体（一个立方体和一个球体），相对于摄像机而言球体位于立方体的前方，像素深度符合预期。

https://picx.zhimg.com/80/v2-931e73ae4283caf9412196eaf837b81f.png

Fig. 3.2.3a

如果我们将球体放置在立方体后面，深度值也和我们预期的一样，为什么呢？因为** Z 缓冲**存储的是屏幕上每个像素的深度值，深度值是根据物体与相机之间的深度距离计算得出的。

https://picx.zhimg.com/80/v2-6fd2325002b2b6e0ee9147786b789b31.png

Fig. 3.2.3b

现在，如果我们将深度测试设置成“总是（Always）”会发生什么呢？在这种情况下，深度测试并不会发生，所有像素在屏幕上显示的深度是相同的。

https://picx.zhimg.com/80/v2-18f4d71f1a5a95de290e65bcf96155c5.png

Fig. 3.2.3c

深度测试的语法如下所示：

1
2
3
4
5
6
7
8
9
Shader "InspectorPath/shaderName" 
{ 
    Properties { … } 
    SubShader 
    { 
        Tags { "Queue"="Transparent" "RenderType"="Transparent" } 
        ZTest LEqual 
    } 
}

3.2.4 | ShaderLab模板

3.2.5 | ShaderLab Pass

3.2.6 | CGPROGRAM/ENDCG

3.2.7 | 数据类型

3.2.8 | Cg/HLSL编程

3.2.9 | Cg/HLSL Include

3.3.0 | Cg/HLSL顶点输入&输出

3.3.1 | Cg/HLSL变量与连接向量

3.3.2 | Cg/HLSL顶点着色器

3.3.3 | Cg/HLSL片元着色器

3.3.4 | ShaderLab回退

其他概念与实现

4.0.1 | 着色器和材质的关系，好有一比啊~

4.0.2 | 我们的第一个Cg/HLSL着色器

4.0.3 | 为Cg/HLSL着色器加上透明度

4.0.4 | HLSL函数的结构

4.0.5 | Shader Debug

4.0.6 | 添加URP兼容

4.0.7 | 内置函数

4.0.8 | Abs函数

4.0.9 | Ceil函数

4.1.0 | Clamp函数

4.1.1 | Sin与Cos函数

4.1.2 | Tan函数

4.1.3 | Exp、Exp2与Pow函数

4.1.4 | Floor函数

4.1.5 | Step与SmoothStep函数

4.1.6 | Length函数

4.1.7 | Frac函数

4.1.8 | Lerp函数

4.1.9 | Min与Max函数

4.2.0 | 时间与动画

第二章 | 光照、阴影与表面

章节介绍

5.0.1 | 配置输入与输出

5.0.2 | 向量

5.0.3 | 点乘

5.0.4 | 叉乘

表面

6.0.1 | 法线贴图

6.0.2 | DXT压缩

6.0.3 | TBN矩阵

光照

7.0.1 | 光照模型

7.0.2 | 环境光颜色

7.0.3 | 漫反射

7.0.4 | 镜面反射

计算机图形学中，最常用的一种反射模型是由 裴祥风（Bui Tuong Phong） 发明的 Phong 模型，该模型根据模型的法线实现了镜面反射。在 Maya 3D 中有一种材质就叫这个名字，可以为模型产生闪亮的表面。

Fig. 7.0.4a

我们可以通过下述等式实现 Phong 模型的镜面反射：

https://picx.zhimg.com/80/v2-52f5711a52419941a465d4fdf832a3d4.png

注意看，这个等式非常像我们在上一小节中学习的兰伯特漫反射公式：

https://pica.zhimg.com/80/v2-eef0e6edcf308ceb265b49b2fa40547a.png

公式中的 [h] 指的是“半程向量”，当它越模型表面的法线 [n] 时，代表反射的亮度越亮。

为了理解这个概念，让我们从模拟镜面反射开始。假设现在我们有一个平面和一束打到平面上的平行光：

https://pic1.zhimg.com/80/v2-839b49f025250fbc6afa123468d17a60.png

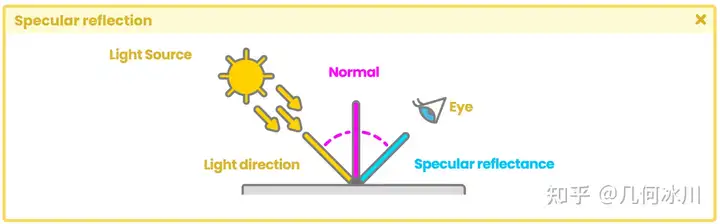
Fig. 7.0.4b

根据上图中的结果，结合初中物理所学的知识，我们可以推断出入射角与反射角的角度相同。这个性质带来了一个问题：如果我们的眼睛（相机）不在反射光的方向上，我们就无法看到它。为了解决这个问题，我们可以根据观察方向，计算出法线和光源入射方向之间的一个中间向量：

https://picx.zhimg.com/80/v2-6ebbe874a3cfe8c99a7a1a1e2098a164.png

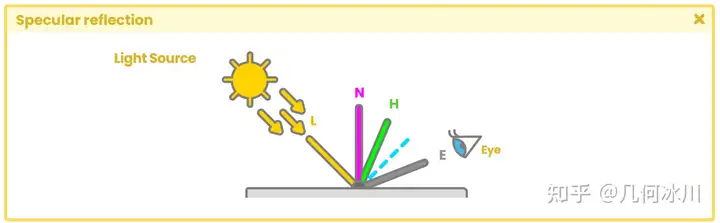
Fig. 7.0.4c

向量 [e] 指的是人眼（相机）的“观察方向”，向量 [h] 即法线和光源入射方向之间的“半程向量”。我们可以通过下面的公式计算半程向量 [h]：

https://pica.zhimg.com/80/v2-4c2f7b14ad966815d9ee64a39c1de9f5.png

值得一提的是，我们的程序中需要使用归一化后的向量，这代表向量的大小为“1”。因此，上述公式可以写作：

https://pica.zhimg.com/80/v2-ffa8862b9e55d5568ccf90360d7777ba.png

在反射的计算中，我们需要用到至少三个变量，分别是：

• 光照方向
• 表面法线
• 半程向量（包含了视线方向）

另外，如果我们想要加上高光贴图，我们将会需要计算反射颜色。

让我们创建一个名为 USB_specular_reflection 的 无光照着色器 。值得一提的是，这个着色器中的许多操作与上一小节中的 **USB_diffuse_shading **着色器是一样的，因此我们可以从头开始编写，也可以继续使用上一节中的着色器。

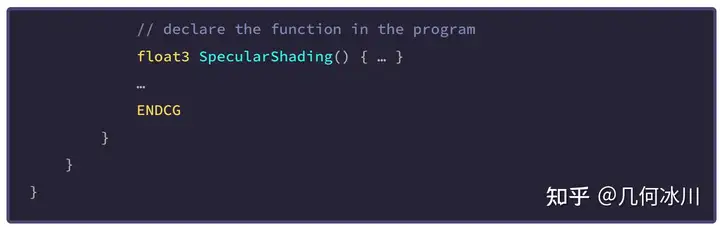
在程序中，让我们创建一个名为 SpecularShading 的函数，包含了我们在前文中提到的几个属性：

https://picx.zhimg.com/80/v2-e77448556e23bd83d19e42661b7a2cdb.png

https://picx.zhimg.com/80/v2-f17fee8a9e2305332e4fe3110a352c0f.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// internal structure of the SpecularShading function 
float3 SpecularShading 
( 
    float3 colorRefl, // Sa，镜面反射颜色
    float specularInt, // Sp，镜面反射系数
    float3 normal, // n，模型表面法线
    float3 lightDir, // l，光线角度
    float3 viewDir, // e，观察角度
    float specularPow // exponent，指数
) 
{ 
    float3 h = normalize(lightDir + viewDir); // 半程向量

    return colorRefl* specularInt * pow(max(0, dot(normal, h)), specularPow); 
}

在上面的代码中，我们声明了一个名为 SpecularShading 的函数，该函数返回一个包含 RGB 颜色的三维向量。在它的参数中，我们可以找到反射光颜色（colorReflRGB）、镜面反射强度（specularInt [0, 1]）、模型表面法线（normal XYZ）、光照方向（lightDir XYZ）、观察方向（viewDir XYZ）和镜面反射指数（specularPow [1, 128]）。

就像我们在上一小节中所做的那样，我们需要使用世界空间下的模型法线、观察方向和光照方向，因此需要在顶点着色器阶段完成一些变换操作。

让我们在着色器中配置三个属性：纹理类型的高光贴图、[0, 1] 范围的镜面反射强度和 [1, 128] 范围的镜面反射指数：

https://pic1.zhimg.com/80/v2-52258fd709021e435a339a9e639eb411.png

与 _MainTex 属性不同的是，_SpecularTex 的默认值是黑色，这一点可以从语句末尾的“black”中得到印证。如果我们不从 Unity 检查器中指定纹理，那么模型看起来就会是黑色的。

请注意，镜面反射将被加到主纹理中，因此在这种情况下，黑色在图形上是不可见的，因为黑色等于“0”，而 0 + 1 = 1。

https://pica.zhimg.com/80/v2-bf529d79d7c0482b9d3ea83f2d84b544.png

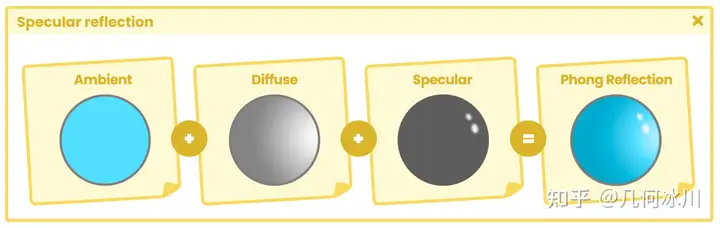
Fig. 7.0.4d

接下来，我们需要声明三个属性的连接变量：

https://pica.zhimg.com/80/v2-f3be529609594b2f14947de4665e99ad.png

为什么我们在上面的代码中注释掉了 _SpecularTex_ST ？我们已经学习过，连接变量末尾的“ _ST ”为纹理加上了平铺和偏移，而一般来说，高光贴图** _SpecularTex** 不需要这两种变换。

我们还写了一个名为 _LightColor[n] 的连接变量，改变量将与 _SpecularTex 的颜色相乘，这样镜面反射的颜色就会被场景中的光源颜色所影响了。

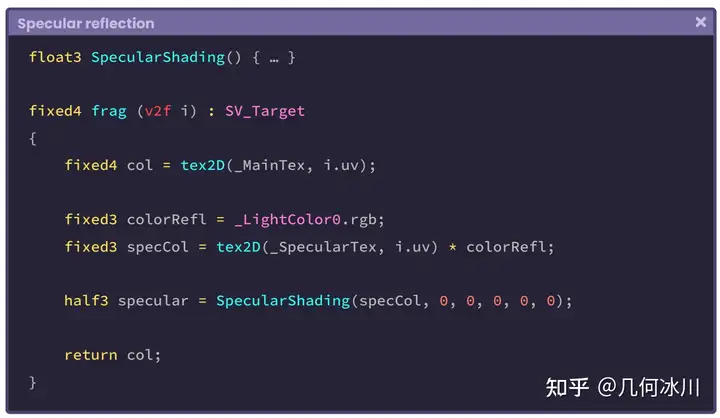
现在属性们已经准备好了，我们可以开始在片元着色器中使用 **SpecularShading **函数了。让我们从计算反射光颜色开始：

https://pic1.zhimg.com/80/v2-bb40396b828d9e2899a21a3390eb6e96.png

SpecularShading 函数的第一个参数代表了反射光颜色（Sa）。我们将高光贴图 _SpecularTex 与光源颜色（colorRefl）相乘，并将结果储存到名为 specCol 的三维向量中，传入函数的第一个参数。

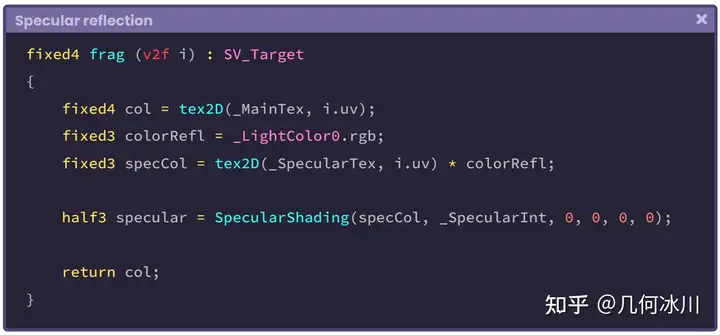
第二个参数代表反射强度，我们可以直接使用属性 _SpecularInt ，范围为 [0, 1]：

https://pica.zhimg.com/80/v2-56bd0b34850e8f5a5dcfac361e38e520.png

函数的第三个参数代表世界空间下的模型法线。我们需要将法线同时加入顶点输入与顶点输出中，并在顶点着色器阶段将法线变换到世界空间，这和我们在上一小节中所做的步骤相同。

让我们从配置顶点输入开始：

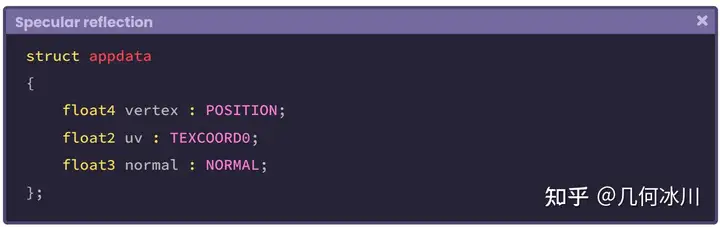
https://pic1.zhimg.com/80/v2-e458286735c4aa0b5e4371299a33f4b7.png

接着，我们需要在顶点输出中配置法线。然而，顶点输出结构体并不包含 NORMAL 语义，因此我们需要为法线配置四维语义 TEXCOORD[n]：

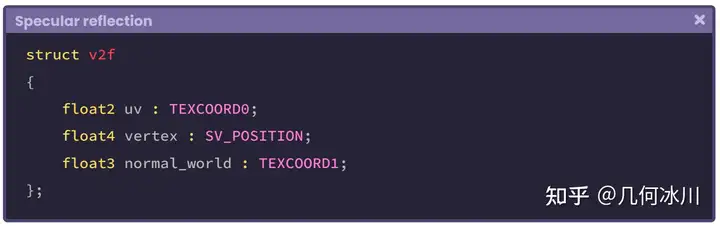
https://pic1.zhimg.com/80/v2-2cc8325dd946c3d13c1213380ec1ae87.png

在回到片元着色器之前，我们还需要在顶点输出中配置最后一项输出，该属性将被用于计算观察方向的参考点。

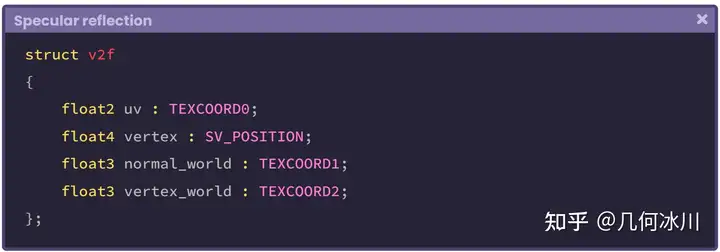
https://pic1.zhimg.com/80/v2-64814ac9952d8c2dc3d200786be5300e.png

如上述代码所示，我们添加了一个名为 vertex_world 的新属性，代表了模型顶点在世界空间中的位置。

接着，我们来到顶点着色器中，对顶点与法线进行变换。与之前不同的是，我们现在直接使用 UnityObjectToWorldNormal 函数直接将法线从模型空间变换到世界空间：

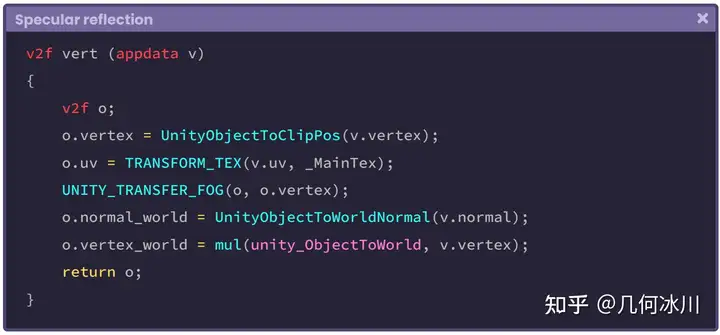
https://picx.zhimg.com/80/v2-07c6c25f4eaf4eb61ae4185cd28da1dd.png

UnityObjectToWorldNormal 函数被包含在 UnityCg.cginc 中，与将 _ObjectToWorld 矩阵与模型法线相乘的结果一致。让我们看看这个函数的内部结构（译者注：这里的norm不是范数，就是normal的简写）：

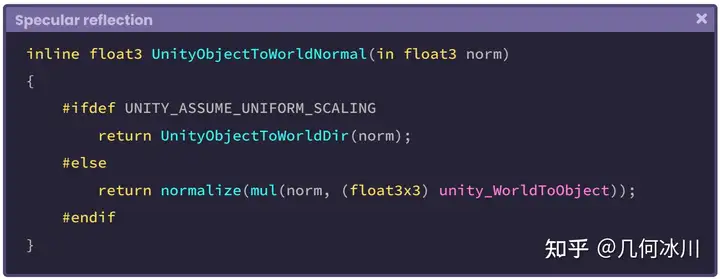
https://pica.zhimg.com/80/v2-695c6f0a4dd05305e57f06c363582431.png

需要注意的一点是，函数对 normal_world 进行了归一化处理，因此现在法线是一个大小为“1”的三维向量，代表世界空间中的一个方向。而 vertex_world 世界空间中的一个点（位置）。

让我们回到 SpecularShading 函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    // 我们已经将法线变换到了世界空间
    float3 normal = i.normal_world; 
    fixed3 colorRefl= _LightColor0.rgb; 
    fixed3 specCol = tex2D(_SpecularTex, i.uv) * colorRefl; 

    half3 specular = SpecularShading(specCol, _SpecularInt, normal, 0, 0, 0); 

    return col; 
}

我们可以看到，在片元着色器中我们创建了一个名为 normal 的新三维向量，获取了顶点输出中变换到了世界空间的法线。接着，我们将其传入到 SpecularShading 函数中作为第三个参数。

因为我们可以直接使用内部变量 _WorldSpaceLightPos[n] 来表示 *世界空间 *中的光照方向，因此不需要对光线进行任何变换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    // 让我们来计算光线方向
    float3 lightDir = normalize(_WorldSpaceLightPos0.xyz); 
    float3 normal = i.normal_world; 
    fixed3 colorRefl= _LightColor0.rgb; 
    fixed3 specCol = tex2D(_SpecularTex, i.uv) * colorRefl; 

    half3 specular = SpecularShading(specCol, _SpecularInt, normal, lightDir, 0, 0); 

    return col; 
}

现在我们只需要计算观察方向就好了，因为 SpecularShading 函数的最后一个参数对应镜面反射指数（specularPow），用于增加或减少反射。

为了计算观察方向，我们需要用世界空间下的相机位置减去世界空间下的模型顶点。Unity 提供了一个名为 _WorldSpaceCameraPos 的内置变量，这样我们就能精确地获取世界空间下的相机位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    // 让我们来计算光线方向
    float3 viewDir = normalize(_WorldSpaceCameraPos - i.vertex_world); 
    float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);
    float3 normal = i.normal_world; 
    fixed3 colorRefl= _LightColor0.rgb; 
    fixed3 specCol = tex2D(_SpecularTex, i.uv) * colorRefl; 

    // 将观察方向传入函数
    half3 specular = SpecularShading(specCol, _SpecularInt, normal, lightDir, viewDir, _SpecularPow); 

    return col; 
}

最后一步是将函数计算得到的镜面反射结果添加到主纹理上：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 
  
    float3 viewDir = normalize(_WorldSpaceCameraPos - i.vertex_world); 
    float3 lightDir = normalize(_WorldSpaceLightPos0.xyz); 
    half3 normal = i.normal_world; 
    fixed3 colorRefl= _LightColor0.rgb; 
    fixed3 specCol = tex2D(_SpecularTex, i.uv) * colorRefl; 

    half3 specular = SpecularShading(specCol, _SpecularInt, normal, lightDir, viewDir, _SpecularPow); 
  
    // 让我们将镜面反射加到纹理上
    col.rgb += specular; 

    return col;
}

请记住，我们不能直接将一个四维向量与一个三维向量相加，所以我们需要确保只将镜面反射结果加到了主纹理的 RGB 通道上。

由于镜面反射是一种光照传递，我们必须再次进入 标签（Tags） 语义块，以配置漫反射的方式配置渲染路径：

7.0.5 | 环境反射

7.0.6 | 菲涅尔效应

菲涅尔（Fresnel） 效应（由奥古斯丁-让·菲涅耳发现）也被称为边缘效应（Rim effect），是一种反射，其大小与物体法线与相机方向的夹角成正比。

https://pic1.zhimg.com/80/v2-39bce8e1195abe3adbafe644b83d3a81.png

Fig. 7.0.6a

模型表面距离相机越远，菲涅尔反射就越多，因为入射方向（相机）与物体法线之间的角度越大。

https://pica.zhimg.com/80/v2-c15465cdeaed6503f3ae91966d7f0414.png

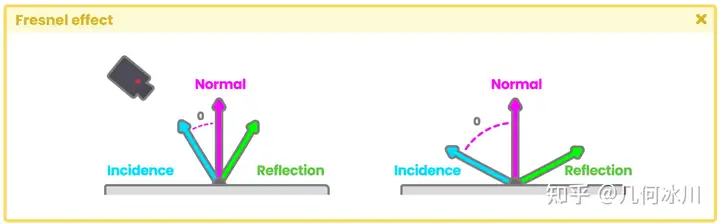
Fig. 7.0.6b

当入射方向（相机）与法线之间的夹角为“0°”时没有反射存在，因为两个向量是平行的。当入射方向与法线之间的夹角为“90°”时全反射，两个向量相互垂直。这非常有趣，因为当没有反射时函数返回黑色，全反射时则返回白色，这些值对应于像素的最大和最小光照值。

为了理解这个概念，我们需要分析来自 Shader Graph 中的 Fresnel Effect 节点函数。

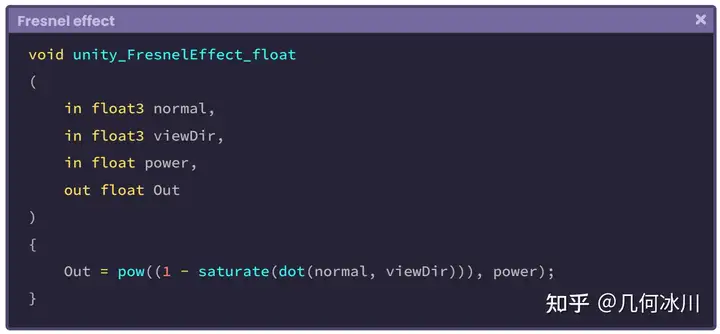
https://picx.zhimg.com/80/v2-d14eb54f66b1aff3564dded4a19a4220.png

在这个函数中发生了一些事情，我们将在本节中进行详细介绍，现在我们暂时先只关注输出的内部操作。这一操作可分为三个过程：

https://picx.zhimg.com/80/v2-2905ed31bdb07dc0431eaea74bd3d5ce.png

这个操作将确定入射方向与模型法线之间的夹角，并返回范围在 0 ~ 1（[0.0f, 1.0f]）之间的数。

我们已经知道，“点乘（dot）”函数根据夹角的值将返回计算结果。由于反射操作只需要一个介于“0”和“1”之间的值，因此我们添加了函数 saturate ，以限制这个范围之间的值。

1
2
3
4
5
6
7
8
9
10
11
// 最小返回“0”，最大返回“1”
float saturate (float x) 
{ 
    return max(0, min(1, x)); 
} 

// 允许设置最小值与最大值的区间
float clamp (float x, float a, float b) 
{ 
    return max(a, min(b, x)); 
}

Saturate 函数与 clamp 函数功能类似，不同之处在于后者可以修改最小值和最大值来控制范围。

让我们从“1 - x”继续。

https://picx.zhimg.com/80/v2-0cd7962d39abeae670d26dfa15128c27.png

要理解这个操作的本质，我们必须回到之前的练习。当视线方向和表面法线平行且指向同一方向时，点乘将返回 “1”。这对我们来说是个问题，因为我们需要该操作返回“0”，也就是黑色。

https://pic1.zhimg.com/80/v2-47b1394cf780133a1ba87f5e6ebbaf7f.png

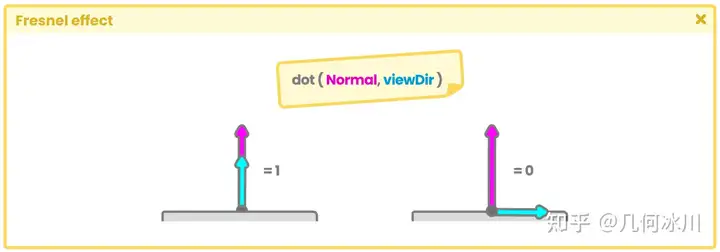
Fig. 7.0.6c

而“1 - x”运算具有如下翻转结果的功能：

1
2
3
4
5
6
7
// 如果法线和视线方向在同一方向上平行 
saturare(dot(float3(0, 1, 0), float3(0, 1, 0))) = 1 
1 - 1 = 0 

// 如果法线和视线方向垂直 
saturare(dot(float3(0, 1, 0), float3(1, 0, 0))) = 0 
1 - 0 = 1 

最后，在函数中，我们可以找到“ pow(x, power) ”运算。该运算允许我们增加或减少反射的范围。

让我们创建一个名为 USB_fresnel_effect 的无光照着色器帮助我们更好的了解 Shader Graph 中的 Fresnel 节点中的操作。让我们在着色器中加入以下代码：

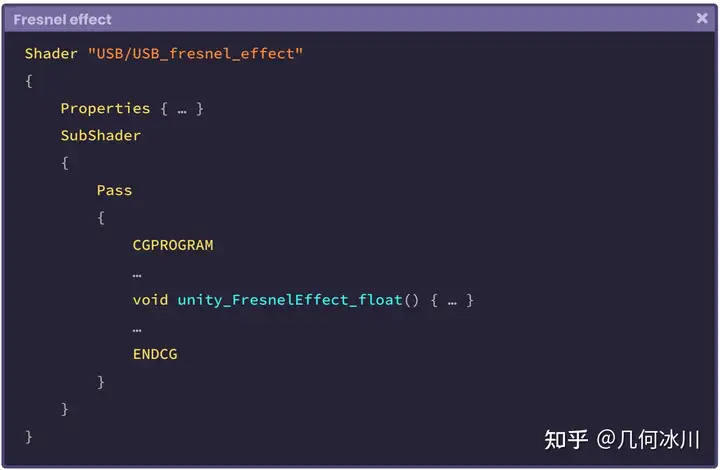
https://picx.zhimg.com/80/v2-a7a581d0ce31405771910ef1f5c9bdaf.png

需要注意的是，函数 unity_FresnelEffect_float 的返回类型是“ void ”，在第 4.0.4 小节中我们曾学习了无返回值和有返回值的函数的区别。在上述的代码中，我们声明了一些变量，并将它们作为参数传入函数中。

让我们在片元着色器中声明该函数。

1
2
3
4
5
6
7
8
9
10
11
void unity_FresnelEffect_float() { … } 

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    // 初始化无返回值函数
    unity_FresnelEffect_float(0, 0, 0, 0); 

    return col; 
}

函数的第一个参数代表了物体在世界空间的法线，所以我们需要在顶点输入的结构体中使用 NORMAL 语义，并在顶点着色器阶段变换法线的坐标空间。

由于我们需要在片元着色器中使用法线，因此需要在顶点输出结构体中声明一个向量用以存储变换后的法线。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 顶点输入
struct appdata 
{ 
    float4 vertex : POSITION; 
    float2 uv : TEXCOORD0; 
    float3 normal : NORMAL; 
};

// 顶点输出
struct v2f 
{ 
    float4 vertex : SV_POSITION; 
    float2 uv : TEXCOORD0; 
    float3 normal_world : TEXCOORD1; 
    float3 vertex_world : TEXCOORD2; 
};

顶点输出结构体中的向量 vertex_world 用于计算视线方向。

如果我们多加留心，就会发现上面的步骤和前面学习反射的小节中所演示的代码一致。

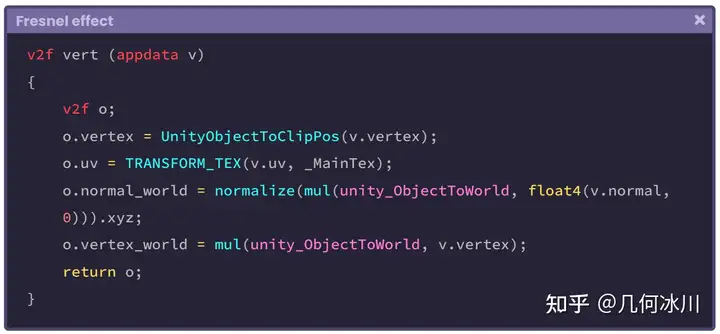
https://picx.zhimg.com/80/v2-15b6928809add885cf44f4e4a9ea95b6.png

现在让我们来到片元着色器中声明两个向量，一个代表法线、另一个代表视线方向。

1
2
3
4
5
6
7
8
9
10
11
12
fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    float3 normal = i.normal_world; 
    float3 viewDir = normalize(_WorldSpaceCameraPos - i.vertex_world); 

    // 将法线与视线方向传入函数中
    unity_FresnelEffect_float(normal, viewDir, 0, 0); 

    return col; 
}

在上面的例子中，三维向量 normal 已经存储了世界空间的法线值；另一个三维向量 viewDir 则计算了视线方向，两个向量均作为参数传入 unity_FresnelEffect_float 函数中，并将在函数内的计算中被使用。第三个参数是“菲涅尔指数”，我们可以传入一个范围来控制反射的范围。

https://pica.zhimg.com/80/v2-74dd5a8c6c4ce39f3d2e17bc4052ec4d.png

我们将 _FresnelPow 属性作为函数的第三个参数。作为一个指数值，我们将使用 _FresnelInt 属性来增加或减少对象中的菲涅尔效应的量。接着，我们需要在程序中为这两个属性声明连接变量：

https://pica.zhimg.com/80/v2-06c7541796c7c267e35555b05d0136c3.png

这一步完成之后，属性与后续的着色器程序产生关联，我们就可以在 Unity 的检查其中动态修改它们了。现在，我们将 _FresnelPow 作为第三个参数传入函数中。

1
2
3
4
5
6
7
8
9
10
11
12
fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    float3 normal = i.normal_world; 
    float3 viewDir = normalize(_WorldSpaceCameraPos - i.vertex_world); 

    // 将指数值传入函数中 
    unity_FresnelEffect_float(normal, viewDir, _FresnelPow, 0); 

    return col; 
}

第四个参数对应的是函数输出值，我们将在这里保存颜色输出。为此，我们只需在函数中创建并添加一个浮点数类型的变量：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    float3 normal = i.normal_world; 
    float3 viewDir = normalize(_WorldSpaceCameraPos - i.vertex_world); 
    // initialize the color output in black 
    float fresnel = 0; 

    // 添加输出颜色
    unity_FresnelEffect_float(normal, viewDir, _FresnelPow, fresnel); 

    col += fresnel * _FresnelInt; 
    return col; 
}

在上面的例子中，我们声明了一个名为 fresnel 的变量并赋值为“0”（黑色），它作为第四个参数被传入函数中并作为其输出值，即 unity_ FresnelEffect_float 函数的最终运算结果。

完成编写后，我们就可以看到菲涅尔反射的效果了。由于其强度（ _FresnelInt ）已被添加到名为“col”的基本纹理颜色中，这样就为场景中的物体增加了反射效果，同时也允许我们修改其强度值。

7.0.7 | 标准表面着色器的结构

7.0.8 | 标准表面着色器的输入与输出

阴影

8.0.1 | 阴影映射

8.0.2 | 阴影投射

8.0.3 | 阴影贴图

8.0.4 | 阴影实现

8.0.5 | 内置渲染管线下的阴影贴图优化

8.0.6 | 通用渲染管线下的阴影映射

Shader Graph

9.0.1 | 什么是Shader Graph

9.0.2 | 准备Shader Graph环境

9.0.3 | 界面分析

9.0.4 | 我们的第一个Shader Graph

9.0.5 | Graph检查器

9.0.6 | 节点

9.0.7 | 用户自定义函数

第三章 | 计算着色器、光线追踪与球体追踪

高级概念

10.0.1 | 计算着色器的结构

10.0.2 | 我们的第一个计算着色器

10.0.3 | UV坐标与贴图

10.0.4 | 缓冲

球体追踪

11.0.1 | 用球体追踪实现函数

11.0.2 | 纹理投影

11.0.3 | 曲面间平滑

光线追踪

12.0.1 | 在HDRP中配置光线追踪

12.0.2 | 在场景中使用光线追踪

• Previous
  2024年读书列表
• Next
  2024年梦境